Of the
many Outer World dimensions, the sensors sense dimensions 1,..,.k., producing
sensory inputs s1, ...,sk to the perceptual function. We can set the perceptual
function to beOf the
many Outer World dimensions, the sensors sense dimensions 1,..,.k., producing
sensory inputs s1, ...,sk to the perceptual function. We can set the perceptual
function to be
p=f(c1*s1+...+ck*sk),
where the squares of the coefficients ci that define the Complex Environmental Variable sum to unity.
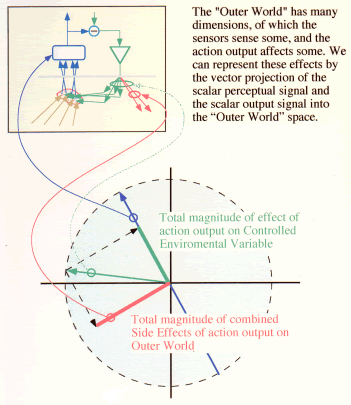
The disturbance (d) also influences dimensions 1,...,k. The output (o) of the control unit affects dimensions 1,...,k in opposing the disturbance, but additionally it affects other dimensions (m,...,n). We assume additivity between the output signal and the disturbance along dimensions 1,...k,, so that si=o*ai+di. The coefficients ai represent the strength of the output influence on dimension i of the Controlled Environmental Variable.
The output affects not only dimensions 1,...,k, but also other aspects of the world represented by dimensions m, ...n. So when we scale the weights of the output influences on the different dimensions by setting the sum of aj^2 to unity, we have to sum over all dimensions, 1, ...,n, rather than over 1,...,k.
These relations are shown in the circular figure. The vector representing the ci is the blue arrow.The vector representing the ai is the green arrow point leftward. The part of the output that affects the controlled perception (ai,...al) is shown by the green bar laid along the blue arrow, and the wasted output that affects the rest of the Outer World (am,...an) is the red bar orthogonal to the blue arrow. The red bar represents the side-effects. Optimally, all the am,...an are zero--that is, there are no side effects and all the energy of the output (represented by a1,...,ak) is used to oppose the disturbance.
