Part 3. Interactions and Reorganization

Contents:

Several kinds of ways in which two control units may interact were discussed earlier. Now we look into how these interactions affect the reorganization of individual units in the context of each other, to make a social structure built of modular substructures.

Conflict

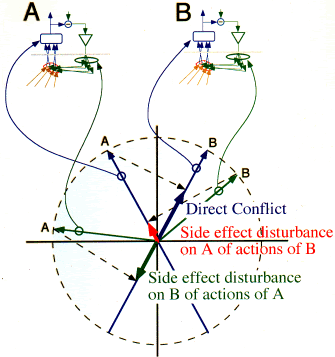
Conflict and mutual disturbance between two independent control units

The vector diagram superimposes the perception and output vectors of two independent control systems, A and B. The diagram ought really to be drawn in four dimensions, two for the perceptual vectors of the two control units, and two for the two output influence vectors. However, examination of this two-dimensional representation may illustrate the main points.

The perceptual vectors of A and B are correlated. This means that if each individually is an optimum controller. the control action of one would disturb the other. In order for the control action of, say, A not to disturb the perception of B, the output vector of A must be orthogonal to the perceptual vector of B. This means that A will not be an optimum controller, since it will have other side-effects on the world, wasting energy. But it will not disturb B.

The problem with this is that there is no signal in either control unit that indicates how much it disturbs the other. If that is to be a criterion for reorganization, it must be a signal based on observation of both A and B, by some other entity. If the mutual disturbance affects the stability of intrinsic variables, then reorganization may create sub-optimal non-interfering control units, but reorganization based only on the ability of each unit to control will never do so.

Mutual disturbance

Two control units can "get out of each other's way" by moving their output vectors, but only at the cost of inefficiency. When there are more than two control units that might disturb one another, it becomes more difficult to find output vector directions that are orthogonal to all the perceptual function vectors of the other control units. Avoiding mutual disturbance then becomes much easier by ensuring that the perceptual vectors are orthogonal and each unit controls optimally. However, again it is impossible for any unit to determine that its perceptual vector is or is not correlated with any other. What can happen, however, is that within the group as a whole control is improved as the correlations decrease. This means that if the side effects of control are serving to control intrinsic variables, that control will be improved by orthogonalizing the set of control units.


In a high-dimensional space, it is almost certain that two vectors in randomly chosen directions will be nearly orthogonal. Specifically, the action vector of any one control system is likely to be almost orthogonal to the perceptual vector of another. But "almost certain" that the vectors are almost orthogonal is not "quite certain" that they are quite orthogonal. In a large set of control units the probabilities turn the other way, and it becomes almost certain that there will exist some pairs of control units for which the output vector of one is highly correlated with the perceptual vector of another, or in which the two perceptual vectors are themselves highly correlated. The first situation means that the control actions of one unit disturbs the other, whereas the second situation puts the two control units into direct conflict.

Reorganization therefore has at least three different aspects (there are others, too):