Structures of Autonomous Perceptual Control Systems

Reconstruction of a talk given to the University of Toronto Mathematics Club

October 29, 1997

M. Martin Taylor

This talk has two main conceptual sources:

W.T.Powers. Behavior: The Control of Perception. Aldyne (1973)

"All behavior is the control of perception"

Control here means exactly what is meant by "control" in an engineering context. The claim is that all living things are control systems, not just that they contain control systems.

S. Kauffman. At Home in the Universe: The Search for the laws of Self-Organization and Complexity. Oxford University Press (1995)

When a large number of active things interact, it is almost certain that organized structures will be formed. Kauffman provides many examples, and shows how phase transitions occur with changes in the strength of interactions and with the number of interacting things.

A Quick Overview

Sections:

1. Collective Effects: Spin Glasses and domains

2. Feedback and Control

3. Interactions among Control Systems

4. Resource Limitations--degrees of freedom

Quick Overview

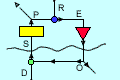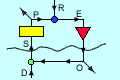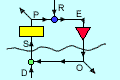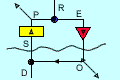Control is taken to be the action of a "control unit". A Control unit takes inputs S from its environment and provides output O that influences the environment so as to affect the state of its inputs (among possibly many other aspects of the environment). The inputs are also influenced by events in the environment of which the control unit has no independent knowledge. These are known as "disturbances" D. The inputs S are converted by a "Perceptual Input Function" into a scalar perceptual signal P which may also serve as an input to other control units. The control unit has a second input, a reference signal R, with which P is compared. The difference between the values of P and R is known as the "error" E, which provides input to an "Output Function" that delivers the output O. O influences S through what is known as the "Environmental Feedback Path." If the influence of O on S is such as to reduce the error E, the value of P tends to track the changing values of the reference signal R. P is the "controlled perception" of the control unit.

If there are two control units controlling quite unrelated perceptions, there is some chance that one of them might affect one of the environmental paths of the other. Its side effects might act as a disturbance to the other, it might be controlling something that is in the feedback path of the other, or it might be controlling something in the path from the disturbance source to the other's CEV. The chance of any of these happening may be very small for any specific pair of control units, but the number of pairs goes up with the square of the number of units, and so does the probability that there exists at least one pair in which the actions of one unit affect the performance of the other.

With enough independent units, the probability approaches unity that there exists at least one pair of units in which the actions of one unit helps the other to control. We are interested only on those interactions in which one unit acts to ease control by another, because reorganization will tend to eliminate the other interactions insofar as the environment makes that possible.

Add a few more units, and the probability is high that there are many cross-influencing pairs. This probability goes up fast since the number of available pairs increases with the square of the number of units. And add yet a few more, and some of the ones that ease the ability of others to control will become part of a chain. A eases B and B eases C. With enough units, at least one such chain will form a loop of mutual support. How many is "enough" depends on the probability that any one will aid any other. Kauffman (At Home in The Universe, Oxford University Press, 1995) talks in terms of probabilities on the order of 10^-6, to give you an idea.

I often use a somewhat strained example to illustrate a two-link loop. Imagine a small ship in a choppy sea. The cook tries to deep fry a succession of batches of food, but the motion of the boat means he can use only small quantities of oil, to avoid splashing. The helmsman tries to keep a straight course, which would help the cook if it could be done, but the waves make keeping straight rather difficult.

Now the cook tosses his used oil overboard. That smooths the waves a bit, making it easier for the helmsman to keep the boat on course. That makes it easier for the cook to use more oil for the next batch of fry-up, which means more oil to smooth the waves for the helmsman, and so forth. Neither knows anything of the effect his actions have on the other, but so long as the cook keeps cooking and the helmsman keeps steering, both have an easier job than if the other was off-duty.

Such loops of mutual support must occur if there are sufficient numbers of independent control units working in a constrained environment, no matter how small the probability that the actions of one will help another to control. In fact, Kauffman shows that in the generic case, there is a phase transition at some number N, where below N the probability is near zero, and above N the probability is near unity, with almost everything linked to everything else directly or indirectly.

So far, the association of control units in a mutually supportive loop is purely accidental. But think what happens if there is only one such loop and one of the control units in it is removed. All of the control units in the loop then find that their work is more difficult--not just the one immediately influenced by the one that went missing. Less drastically, if one reorganized so as to produce different side-effects, it would find that its own control became more difficult (because it broke the loop), and would be likely to reorganize back again (although the other loop members, finding their control diminished, would also be reorganizing, until some new loop might form rather than the old one re-forming).

Such loops must be self-stabilizing, in the same way that adding a second level of control aids the work of the first-level controllers in a hierarchy. Subordinate loops may, for example, exist to restore gaps in the loop. We begin to get into social structures self-organized firstly by the purely random occurrence of assistance loops, and secondarily by the process of reorganization.

Now consider loops built not with individual control units, but with hierarchic organisms. A new-born organism is born into a "society". If the baby organism acts in certain ways, the other members of the society act in ways that bring the baby's perceptions near their reference levels. If the baby acts in other ways, the other members of the society act so that at least some of the baby's perceptions move away from their reference levels (if you want to call that "coercion" it's fine by me; it's just what always happens in any environment, whether that environment consist of other control systems or of inanimate objects). The baby tends to reorganize so as to avoid the actions that spoil its ability to control. Or to put it another way, it learns to be a "responsible" member of the society. It has no "intrinsic variable" need for socialization, but if it does socialize properly as expected for its age, it gets its perceptions better under control than if it doesn't. It helps others, and they help it. It learns the language and the culture into which it is born, as if there were some innate drive for it to do so, though there need be none.

(Parenthetically, one may argue that helping one another without expectation of a direct quid pro quo is the mature expression of this. It results in the same kind of mutual support loops that benefit everyone as those I discussed a couple of paragraphs ago. That's why I consider Jesus as one of the great economists of history, when he said "Cast your bread upon the waters, and it will return to you many times over." Or something like that. It's the antithesis of the economic theories that blight our current global economy by starving the poor, since they are based on getting the most you can and giving the least).

Part 1. Spin Glass

A Spin Glass consists of a set of entitites, each of which has a property whose value is influenced to be like that of its neighbours, here represented by a vector direction.

The property can be anything. In physics it is often the direction of electron spin in a ferromagnet, and the boundaries define magnetic domains. But it could be such a thing as a personal attitude, perhaps toward a social or religious convention, since a person is likely to conform to the views and practices of family, friends, and neighbours.

Conflicting influences are experienced by entities near domain boundaries.
The influence strength of one entity on its neighbour can be thought of as a coupling constant. When the coupling is weak (e.g. when most people are tolerant of cultural and religious differences) domains can interpenetrate. But so long as there is some influence, there will be a tendency for domains to form and to maintain themselves. The value of the "vector" property characteristic of any entity will tend toward that of the majority of the entity's neighbours.

There can, of course, be coupling relations in which each entity prefers an orientation opposed to that of its neighbours. In physics, this is the situation in an anti-ferromagnet. Similar possibilities exist for the more "social" properties that we consider in the following pages, but we will not pursue them yet.

A new-born organism is born into a "society". If the baby organism acts in certain ways, the other members of the society act in ways that bring the baby's perceptions near their reference levels. If the baby acts in other ways, the other members of the society act so that at least some of the baby's perceptions move away from their reference levels (if you want to call that "coercion" it's fine by me; it's just what always happens in any environment, whether that environment consist of other control systems or of inanimate objects). The baby tends to reorganize so as to avoid the actions that spoil its ability to control its perceptions. Or to put it another way, it learns to be a "responsible" member of the society. It has no "intrinsic variable" need for socialization, but if it does socialize properly as expected for its age, it gets its perceptions better under control than if it doesn't. It helps others, and they help it. It learns the language and the culture into which it is born, as if there were some innate drive for it to do so, though there need be none.

The baby belongs to a societal domain in the same sense as an atom belongs to a magnetic domain. If it behaves in ways unsuited to the domain, it is less able to control than if it conforms, and therefore reorganization pulls its "vectors" back into line. If the same baby had been born somewhere else, it would grow up to belong to a different domain--a different "culture." But after a century of easy intercontinental travel and mass migration, many babies grow up influenced by many different cultures. We now have a situation akin to that of the second diagram, whereas in earlier centuries almost everyone lived in a well defined domain, akin to those illustrated in the first diagram.

Keep the concept of a Spin Glass in mind as you read through Part 2. The vectors of the glass will return.

Part 2. Feedback and Control

Form of a Control System

A control system, in the sense used in Perceptual Control Theory, consists of a feedback loop in which a scalar-valued signal called the "perceptual signal" is generated from a complex of values of properties in the world outside the control unit. The perceptual signal is compared with a reference value that also comes from outside the control unit. The difference between the perceptual signal and the reference signal is the "error" in the control unit, and it provided the input to an "output function" that affects the entities in the outer world that contribute to the perceptual signal. These entities are also affected by external influences called "disturbances," the impact of which on the value of the perceptual signal is countered by the effect of the output signal of the control unit. The perceptual signal itself can serve as one of the complex of values that contribute to the perceptual signal of another control unit.

Vector Representation

The perceptual function p=p(s1,...,sk) defines the relationship between the value of the perceptual signal and the values of the sensory input values. It therefore defines the Controlled Environmental Variable.

In simple simulations, a useful form for the perceptual function is one often used in neural network simulations: p=f(c1*s1+c2*s2+...+ck*sk), where f is a saturating non-linear function (e.g. logistic). The set of weights {c1,...ck} defines a vector in the "Outer World" space. This vector is the Controlled Environmental Variable. It can be seen as a projector of the perceptual signal into the "Outer World" space. This vector representation will be important in what follows.

Kinds of influence between pairs of control units

The output from a control unit can do more than affect only those entities that contribute to its own perceptual signal. Any effects it has on other parts of the "Outer World" are called "side-effects," because they do not affect anything it can detect. If these side-effects affect another control system, it is usually because they contribute to the other's perceptual signal, in which case they are part of the disturbance against which the other unit must control. But there are other possibilities.

Indirect Control

One control unit can have effects that alter the ability of another to control. One way this can happen is that the actions of one control unit affects not only the environmental variable defined by its own perceptual function, but also the disturbance that impinges on the CEV of the other. This may be because there is some overlap between the CEV of one and source or transmission route of the disturbance of the other. But it could also be because the side-effects of one might inhibit the disturbance to the other.
Two control units could each influence the other in this way, the control actions of each making it easier for the other to control its perception. It is unlikely that this should happen between two randomly chosen control units, but it is possible. Under those circumstances, at least one would indirectly controlling its perception, indirectly because it involved the non-purposeful intervention of the other control unit.

Here is a real-world example. One possible perception controlled by a person might be to perceive oneself as having food. If there were no farmers, and everyone grew their own food, that perception would be greatly disturbed by the vagaries of the weather. Another perception that people might control is to have money. Farming is (or used to be) a way to influence the amount of money one has. By growing and selling food, the farmer controls a perception of having money.

A side-effect of the farmer's control of the "having money" perception is that (by means of various other people controlling other perceptions) food appears in stores. The consumer has a means of controlling a perception of having food that is less subject to the vagaries of the weather than is home gardening.

The weather still can disturb the consumer's control of the "having food" perception, since it affects the price of food in the store. But the weather has much less disturbing effect on the consumer's ability to have food than it would if the farmer were not controlling for having money.

The influence of each control system on the other is through side-effects. The farmer cannot perceive any one consumer, and therefore cannot control any perception related to the consumer. An outside analyst may observe both farmer and consumer, and may note that if the farmer does not produce what the consumer wants, the consumer will not buy, but all the farmer can see of this is that some crops are more effective than others in bringing in money. According to PCT, the farmer is likely to reorganize to increase the financial effectiveness of crop production. The consumer, meanwhile, cannot perceive the farmer, and buys food rather than growing it because that is a more effective way of controlling the "having food" perception--it takes less time, perhaps, and it certainly is less disturbed by variations in the weather.

Farmer and consumer are, in a way, bound together by the side-effects of each other's control mechanisms. If either stopped controlling those perceptions, or started to control them by other means (such as the farmer giving up farming and starting to work on an assembly line making cars to get money), the other would find it much more difficult to control their own perception. But neither directly perceives the effects on the other of their control actions, and therefore the effects are pure side-effects. It is through these and similar side-effects that society as a whole hangs together.

Many different kinds of influence can occur between two control units.Mutually supportive side-effects are one possibility, in which the actions of one unit reduce the influence of a disturbance on the other unit. Here are three more, two of them detrimental to control, one helpful.

Side-Effect Disturbance.

The action vector (in the Outer World) of one unit is correlated with the perceptual vector of another, even though the two perceptual vectors may themselves be orthogonal. The side-effects of one act as simple disturbances to the other. This is very common. Above, side-effects are shown to be possibly helpful, but it is much more likely that what one person does will directly disturb the perceptions of another.

Conflict.

The perceptual vectors of the two units are correlated, so that any attempt by one to control its perception will disturb the other. If there are enough degrees of freedom available to the two control loops, each is likely to be able to retain control, but if the two perceptual vectors are actually parallel in "Outer World Space" (i.e. the two units are trying to control the same variable at different reference values), conflict will occur--and because many control units have output functions that integrate the error, conflict will escalate.

Hierarchy.

The reference value of one control system may be determined (or influenced) by the output signal from another, and it may feed its perceptual signal back to the other's perceptual input function. The "higher" unit determines what perceptual input value it wants to see, and the "lower" unit provides that value to the best of its ability, thereby shielding the higher unit from disturbances that might otherwise buffet it. In a more complex hierarchy, several lower units each contribute to the perceptual signals of several higher units, and the reference values of the lower units are derived from the outputs of all the higher units.

Shielding

Very occasionally, in a large set of control units, it may happen that the actions of one serve to shield the perception of another from some disturbance (recall the example of the farmer and consumer earlier). If this happens, the shielded unit will be better able to control against the remaining disturbances than it would otherwise have been. Such an arrangement will therefore be likely to be stable against reorganization (the winter-leaf phenomenon; the wild wind may remove some leaves from a drift-pile, but with a lower probability than that it will blow a leaf off a bare patch of ground).

Interference and shielding are two ways control units can interact. How strongly they interact may be thought of as a kind of "coupling constant." The notion of coupling constant is very important in what follows.

Vector representation of control and of side-effects in the Outer World

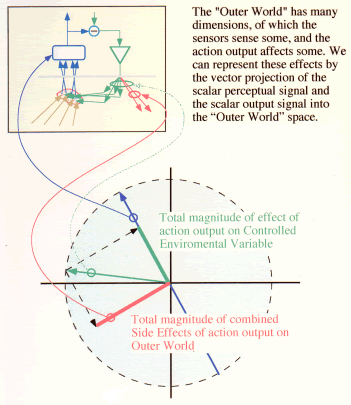Of the many Outer World dimensions, the sensors sense dimensions 1,..,.k., producing sensory inputs s1, ...,sk to the perceptual function. We can set the perceptual function to be

p=f(c1*s1+...+ck*sk),

where the squares of the coefficients ci that define the Complex Environmental Variable sum to unity.

The disturbance (d) also influences dimensions 1,...,k. The output (o) of the control unit affects dimensions 1,...,k in opposing the disturbance, but additionally it affects other dimensions (m,...,n). We assume additivity between the output signal and the disturbance along dimensions 1,...k,, so that si=o*ai+di. The coefficients ai represent the strength of the output influence on dimension i of the Controlled Environmental Variable.

The output affects not only dimensions 1,...,k, but also other aspects of the world represented by dimensions m, ...n. So when we scale the weights of the output influences on the different dimensions by setting the sum of aj^2 to unity, we have to sum over all dimensions, 1, ...,n, rather than over 1,...,k.

These relations are shown in the circular figure. The vector representing the ci is the blue arrow.The vector representing the ai is the green arrow point leftward. The part of the output that affects the controlled perception (ai,...al) is shown by the green bar laid along the blue arrow, and the wasted output that affects the rest of the Outer World (am,...an) is the red bar orthogonal to the blue arrow. The red bar represents the side-effects. Optimally, all the am,...an are zero--that is, there are no side effects and all the energy of the output (represented by a1,...,ak) is used to oppose the disturbance.

Mutual disturbance

Two control units can "get out of each other's way" by moving their output vectors, but only at the cost of inefficiency. When there are more than two control units that might disturb one another, it becomes more difficult to find output vector directions that are orthogonal to all the perceptual function vectors of the other control units. Avoiding mutual disturbance then becomes much easier by ensuring that the perceptual vectors are orthogonal and each unit controls optimally. However, again it is impossible for any unit to determine that its perceptual vector is or is not correlated with any other. What can happen, however, is that within the group as a whole control is improved as the correlations decrease. This means that if the side effects of control are serving to control intrinsic variables, that control will be improved by orthogonalizing the set of control units.


In a high-dimensional space, it is almost certain that two vectors in randomly chosen directions will be nearly orthogonal. Specifically, the action vector of any one control system is likely to be almost orthogonal to the perceptual vector of another. But "almost certain" that the vectors are almost orthogonal is not "quite certain" that they are quite orthogonal. Iin a large set of control units the probabilities turn the other way, and it becomes almost certain that there will exist some pairs of control units for which the output vector of one is highly correlated with the perceptual vector of another, or in which the two perceptual vectors are themselves highly correlated. The first situation means that the control actions of one unit disturbs the other, whereas the second situation puts the two control units into direct conflict.

Reorganization therefore has at least three different aspects (there are others, too):

Part 3. Interactions and Reorganization

Contents:

Several kinds of ways in which two control units may interact were discussed earlier. Now we look into how these interactions affect the reorganization of individual units in the context of each other, to make a social structure built of modular substructures.

Conflict

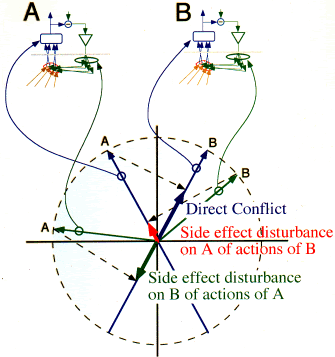Conflict and mutual disturbance between two independent control units

The vector diagram superimposes the perception and output vectors of two independent control systems, A and B. The diagram ought really to be drawn in four dimensions, two for the perceptual vectors of the two control units, and two for the two output influence vectors. However, examination of this two-dimensional representation may illustrate the main points.

The perceptual vectors of A and B are correlated. This means that if each individually is an optimum controller. the control action of one would disturb the other. In order for the control action of, say, A not to disturb the perception of B, the output vector of A must be orthogonal to the perceptual vector of B. This means that A will not be an optimum controller, since it will have other side-effects on the world, wasting energy. But it will not disturb B.

The problem with this is that there is no signal in either control unit that indicates how much it disturbs the other. If that is to be a criterion for reorganization, it must be a signal based on observation of both A and B, by some other entity. If the mutual disturbance affects the stability of intrinsic variables, then reorganization may create sub-optimal non-interfering control units, but reorganization based only on the ability of each unit to control will never do so.

Intrinsic Variables

What perceptions are controlled by such a complex organism as a bacterium, a tree, a worm, or a person? It may seem odd to say that a bacterium controls its "perceptions", but remember the PCT definition of a perception: the value of some variable within an entity (e.g. a control unit) that corresponds to some state or complex of states outside the entity. Even the lowly e-coli bacterium (of which, more later) detects whether it is moving up or down a gradient of nutrient concentration, and varies its direction so as to "perceive" itself to be moving up-gradient.

To survive, any organism must maintain its internal chemistry within certain constraints. But how it can do so must depend on the environment in which the organism finds itself. One thing any human must do is eat. But the means to be in a position to eat are different if the person has to grow or hunt their own food or is in a position to buy it in a shop. Genetics can determine that the reference level for a control system controlling a perception of blood sugar levels should be thus-and-so, but genetics cannot possibly determine the reference levels for the perceptions involved in shopping for food. Accordingly, PCT incorporates a concept of "intrinsic variables" which have genetically determined reference levels in any given species.

The values of the intrinsic variables are affected by external disturbances and by the activities of the organism. Blood sugar is reduced as the cells burn sugar to get energy. The process increases the level of carbon dioxide in the blood, but the activity of breathing reduces that level while increasing the level of oxygen, which is used in the burning that energizes the body. There are many such loops, some well known, others yet to be discovered. They go all the way down to the mechanisms whereby the genes are expressed in the building of proteins, etc. We are not concerned here with those loops. But we are concerned with the larger-scale activities of the body, such as breathing, which was mentioned as a component of one loop. Or shopping, which in some environments could be equally important in keeping blood sugar levels where they should be.

If the perceptions involved in shopping serve to control the intrinsic variables, but many of the relevant control systems cannot be defined genetically, how can they be constructed? PCT suggests a mechanism called "reorganization."

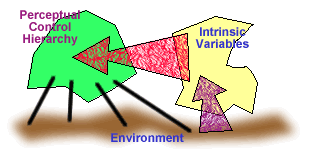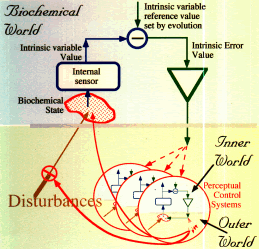These two figures represent (above) a global view of the relation between the intrinsic variables, the perceptual control hierarchy, and the common environment in which they both live; and (right) a local view of one hypothetical intrinsic variable that influences the relationships of some variables in the perceptual control hierarchy, the side-effects of which reduce the effect of a disturbance on the value of the intrinsic variable, or perhaps affect it directly.
When a hierarchy of perceptual control systems is appropriately constructed, the side-effects of its controlling actions result in control of the intrinsic variables.The states of the intrinsic variables affect the structure of the perceptual control hierarchy by reorganizing it if its actions are ineffective; the perceptual control hierarchy's actions affect its environment, and the environment affects the intrinsic variables. The end result is a perceptual control hierarchy that controls perceptions that seem to have little to do with the intrinsic variables. The intrinsic variables are controlled indirectly.

Indirect control can work only in an environment that is sufficiently stable. In an unstable environment, both the actual side-effects and what the side-effects influence may change so that the actions involved in controlling any one perception may influence the intrinsic variables in one direction at one time, and in another direction at another time. On the other hand, if the environment is very stable, some aspects of the overt perceptual control could conceivably be built-in genetically. The laws of physics, for example, say that organisms living on solid ground will be subject to the pull of 1g of gravity. That fact has not changed for as long as life has existed on the Earth. It is a very stable aspect of the environment.

One aspect of "stability" is the stability of perceptual control. If control is not very good, the side-effects will be very variable, and the effect on the intrinsic variables will be inconsistent. If, for example, the transportation system fails and there is little food in the shops, control of the shopping perceptions relating to the perception of having food will be difficult, and the intrinsic variables relating to blood sugar may depart from their reference levels--in plain language, the person may starve. When the food supply is restored, the person's control for having (and eating) food is better, and even though the person does not perceive blood sugar level directly (unless the person is diabetic and has a blood-sugar measuring device), the acts involved in the perceptual control will bring the blood sugar level nearer to its evolutionarily determined reference level.

Stability of perceptual control is tightly linked to the quality of perceptual control. In discussions of PCT, it is often tacitly assumed that a measure of how well the perceptual control hierarchy is performing is one of the intrinisic variables. Indeed, we often consider "learning" to be based on the recognition of our inability to do something we want to do. This suggests that learning can be and often is based on the quality of control, but it also suggests that the quality measure is not an orthodox "intrinsic variable," since those normally cannot be perceived directly.

Learning better control

In the vector representation of the perceptual function and the influences of the output signal in the Outer World, the appropriateness of the control action is represented by the relative orientations of the two vectors. The closer the orientation, the fewer side-effects and the more of the output energy is going into controlling the perception. In this representation, "learning" consists of bringing the vectors representing the perceptual function and the output influences into closer alignment. This could be done by changing the orientation of either. Reorganization could involve learning to perceive something differently, learning to act differently to control a given perceptual signal, or both. (It can also involve other alterations to the structure of the hierarchy, but we are not considering those possibilities here.)

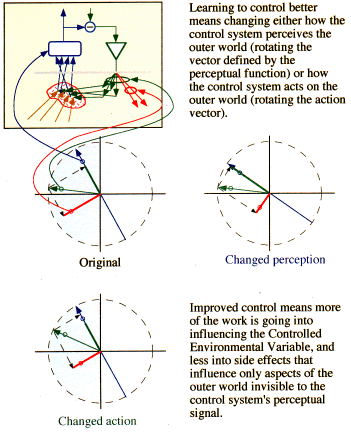
Characterising the learning process in the Vector representation

 

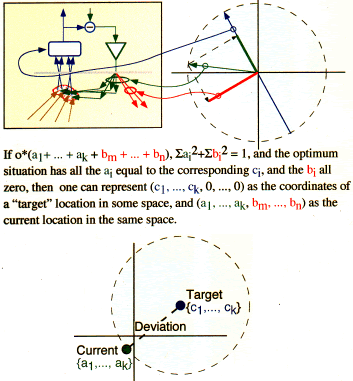Problem

Find the "target" when all that is known is the (scalar) quality of control. The vector components cannot be estimated, nor can the direction to the target.

Approach to a solution (e-coli)

Alter the vector {a1,...ak,bm,...bn} by a unit increment in a random direction. If control improves, alter further in the same direction. If it gets worse, make a new random choice of direction. (Colloquially, in PCT discussions, this is called "e-coli" learning, since it is based on the behaviour of the noxious bacterium).

The rationale for e-coli learning is that there is no a priori way of knowing how to act differently so as to improve control of any particular perceptual signal. It is a classic hill-climbing optimization problem in a high-dimensional space. The hill may not be monotonic, so the e-coli can get stuck in sub-optimum locations. But it is a simple mechanism and fairly robust against minor deviations from regularity in the hill-slope, because there is always going to be some movement away from wherever the e-coli finds itself, even when it is truly at the local (or global) optimum.

One problem with e-coli learning in a very high-dimensional space is that almost all directions are nearly orthogonal to the direction toward the target. This means that progress can be very slow for long periods, interrupted by short bursts of great change. (This is very reminiscent of the progress of evolution generally, with long periods of near stasis followed by bursts of change. It is called "punctate evolution" which has provided evolutionary theorists with considerable numbers of unnecessarily published papers).

Reorganization--The "Winter Leaf" effect

The side-effects of controlling a perception cannot reliably influnece the intrinsic variables unless the perception itself can be reliably controlled. Accordingly, a reasonable surrogate "intrinisic variable" is the effectiveness of control in the environment in which the control unit finds itself. Poor control must be improved, which is what the e-coli mechanism does in a very simple way.

The e-coli mechanism is erratic. The only consistent thing about it is that when it is far from the target it tends to move long distances, but when it is close to the target it moves back and forth without going very far. Its behaviour is like that of a winte leaf in the wind. In open spaces, the leaf is blown along until it finds itself in a place shelteed from the wind, and thee it is likey to stay a while. As a result, winter leaves blow away from most spaces, to pile up in large localized drifts. In the same way, reorganizing control systems drift toward organizations in which they control better than they would in "neighbouring" organizational structures--and in such "good" organization, the chemical (real?) intrinisic variables are also well controlled.

On other grounds, Kauffman has shown that modularization improves the optimization of evolving interacting systems. In the context of control, this means that the space in which e-coli must work, there may not be a very large number of dimensions, and progress toward the target may be reasonably regular.

Coupling Constants: a Flip-Flop arrangment

A "Flip-Flop" is the central element of a computer. It is discussed here for several reasons: Firstly, it illustrates the idea of a coupling constant; secondly, it shows how the behaviour of a structure can vary radically with a minor change in a coupling constant; thirdly, the generalization of the concept of a flip-flop can be important in explaining other phenomena.

The illustration shows the generic connection of a flip-flop. Two elements (which we will later identify with the perceptual input functions of two control units) each have two inputs, one of which comes from outside, while the other comes as an inhibitory input from the output of the opposite element. The two elements are saturating amplifiers, which cannot go more positive or negative than their saturation values. When input A is high, it tends to depress the output of B, which relases A from inhibition, increasing its output. If the gains of the two cross-connection amplifiers are high, only one of the two outputs can be "high" but if the cross-coupling gains are low, each is only moderately affected by the output of the other.

The relationship between the outputs of the two elements, their external inputs, and the coupling constant can be shown as two related 3-D diagrams. The x-axis (left-to-right in the diagram) represents the difference between the A and B external inputs (assuming their sum stays constant). When the A external input is much higher than the B input, the A output is always high and the B output low, but the degree to which this is true depends on the gain of the cross-coupling amplifiers (the coupling constant), shown on the y-axis (in and out of the viewing plane). The outputs are shown separately in the two halves of the diagram, A on the left and B on the right.

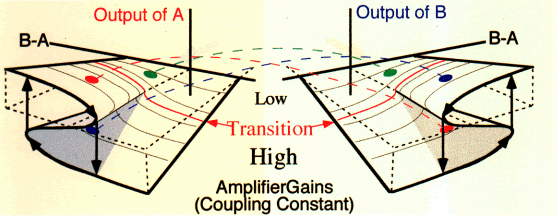
The arrows shown on a path on the near edges of the two diagrams illustrates how changes in data values may affect the values of the two outputs. Suppose A is high and B low with a high coupling constant (red dots), and that the B input is gradually raised. The output traces a path rightward across the upper sheet of the A diagram and the lower sheet of the B diagram until it comes to the reverse curve, at which point it switches abruptly, to the lower sheet of A and the upper sheet of B. If external data are then returned to their former values, the outputs do not. They are at the positions marked by the blue dots, with A staying low and B staying high.

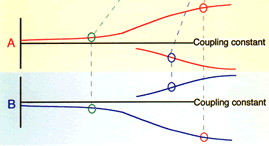The diagram above shows a characteristic phenomenon of such coupled systems--a change in the dynamics that depends on the coupling constant. If the coupling constant is low, as at the condition shown by the green dots, the output values are determined by the external input values. If, however, the coupling constant is above some transition value, there are input values for which the output values split into two possible pairs (shown by the red and blue dots). For such intermediate data values, The transition is called a "bifurcation point" in the dynamics of the coupled system (the diagram at the left shows a slice through the two 3-D diagrams for a particular set of input data values that slightly favours A, but the bifucation point still exists, as shown by the split curves). A is high and B low if that was the situation earlier, or the contrary might also be the case for the same external data input values. The situation will not change until either the coupling constant is reduced, or the external input data values change.

The arrangement here is a single flip-flop. Next we will look at a more complex arrangement, in which two flip-flops are intercoupled so that each can bias the other.

More on Coupling Constants: two mutually supportive flip-flops

This diagram shows two flip-flops. A and B form one, C and D the other. But these flip-flops are interconnected so that A and C, and B and D separately support each other in the sense that if the A output is high it delivers a positive input to help C go high and vice-versa. Similarly for B and D. We assume that these associative coupling constants are small enough that it is possible for A to be high while C stays low, and vice-versa. Otherwise, there might as well be only one flip-flop, either AB or CD. With a small associative coupling constant, if A is high, it takes a smaller input at C to switch the CD flip-flop into the C-high condition than would be the case if B was high and A low.

The connections between A and C, and between B and D, are positive feedback loops. If the coupling constants are too high, the loop gain can go above unity, forcing the whole system into a locked up condition. However, this positive feedback loop is mitigated by the negative loops ACDBA and ABDCA. The whole analysis is complex, but certain aspects are easily seen.

Firstly, we assume that the associative coupling constants are small. What happens then is that if the input to the AB flip-flop is such that the A output is high (A is "seen"), then it is easier to "see C" than it is to "see D." A is "associated" with C, and B with D. One can readily understand this as a simplification of what may happen in everyday "association," and in particular as a kind of labelling, in which seeing A allows the label "C" to be perceived. We will not pursue this further here, but to see the implications, imagine a forest of elements coupled positively and negatively, with relatively low coupling constants, rather than, as here, having two pairs of positively coupled and two pairs of negatively coupled elements. Such an arrangement would show clusters of associations and clusters of mutually inhibitory elements. Think "spin glass."

The issue of interest at this point is simply to illustrate phase transitions and the effects of changing coupling constants. The spin glass effect among coupled perceptual functions will not be pursued, but it could be important in a discussion of control theory in the use of language, among many related psychological phenomena.

Next we examine coupling in the form of catalysis, following Kauffman, to illustrate the effects that can occur when a low-probability phenomenon can occur in large groups of interacting entities.

Catalytic Loops

This section is based almost entirely on my understanding of Stuart Kaffman's book "At Home in the Universe" (Oxford University Press, 1995).

Chemical catalysis may seem a long way from the mutual interactions of control loops, but there is really quite a close connection. A catalyst is a chemical whose presence facilitates a reaction without affecting the continued existence of the catalyst. (Other chemicals may act to inhibit reactions, but we are not concerned with those "anti-catalysts"). As we have seen, the control actions of one control unit may, on occasion, facilitate the ability of a different control unit to control its own perceptions, without the first being affected in any way by the existence of the second. The facilitating unit acts on the second control system as a catalyst does on the reactions it catalyzes.

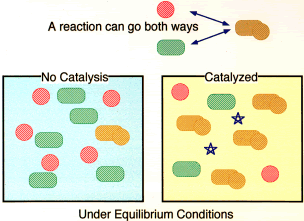A binary chemical reaction can be seen as the combination of two elementary units into a single resulting compound. All such reactions can go both ways: the compound can split into the two elementary units. Under equilibrium conditions, there will be some of the compound and some of the components in the mix. How much there is of each will depend on many conditions, one of which is the presence and quantity of catalyst in the mix.

If a catalyst (stars in the right-hand diagrams) is added that enhances the likelihood that the components will associate to form the compound, there will be more of the compound and less of the components in the equilibrium mix. The more catalyst there is, the more of the compound and the less of the components there will be.

 
The more different components there are in the mix, the more reactions among them there may be, and each reaction produces a reaction product, which could be a component or a catalyst in a quite different reaction.

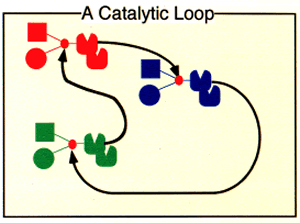The product of one reaction can be a catalyst for a quite different reaction. The product of that reaction can catalyze another, and so forth. Eventually, one of the products may catalyze the original reaction, to complete a loop. If this happens, the loop is self-sustaining. The products of those reactions will increase at the expense of the products of any other reactions involving the same building block components.

It may be highly unlikely that the product of any specific reaction will catalyze any particular other reaction, but if there are enough components (and their reaction products) in the mix, it is almost certain that such a catalytic relationship will exist somewhere in the mix, and with more components and reaction products, at least one loop is almost certain to form.

Reorganization in a Large Group of Control Systems

When there are many control systems, there are many ways each may influence others, most of them by disturbing the perceptions of the others, but some in a beneficial way.

If there is a probability P that one specific control system's actions will benefit a specific other, then the probability that it will benefit at least one other in a group of N is , and the probability that at least one of them will benefit at least one other is 1 - (1-P)^(N*(N-1)). To see how rapidly the probability approaches unity, if P is 10^-5, the probability that there is at least one such link is 0.5 if there are 250 control units, 0.9 if there are 480 units, and over 0.9999 if there are 1000 units.

There is, of course, a much higher probability that any two units will interfere with each other than that one will benefit the other. However, when control is poor, reorganization tends to change control systems and their linkages more than when it is good. This means that beneficial links tend to stay, and even to grow in number, as a consequence of reorganization, whereas interfering relationships tend to be eliminated.

If with N units there is a better than even chance that there will be at least one beneficial relationship, with a very few more units there will very probably be a lot of them. The number of possible relationships increases as N^2. The more links there are, the more likely it is that somewhere there will be a control unit A that benefits control unit B while B benefits C. and with only a few more units, it becomes practically guaranteed that there will be at least one loop, in which A benefits B, B benefits C, ... Z, and Z benefits A.

Reorganization tends to alter relationships, but less so when control is good. Mutually supportive loops enhance the ability of each memeber of the loop to control. Loop members are theefore more likely to retain their characteristics than are control units that "fly solo." In a large structure undergoing continual reorganization, the dominant feature is likely to be sets of mutually supporting control units, and some of those sets will be loops.

Mutual Support Domains

In a large set of control systems if one loop of mutual support can form, so can others. It is quite probable that several independent loops of mutual support may develop. The members of a loop support one another in the same way as do members of a spin-glass domain.

Mutual Support loops as "Domains"

If one of the members of a loop changes its perceptual vector or its action vector, it changes the way it interacts with the other members of the loop, and the control performance of all members of the loop is likely to get worse. Reorganization is therefore likely to restore the loop--or to create another more effective one.This is what makes it like a spin-glass domain.

Or else the loop effectively ceases to exist, leaving its members to "fly solo." Solo control systems may not control well in the environment of the disturbances induced by the actions of the other control systems, and their perceptual or action vectors may be changed by reorganization.

How likely is it that two domains will be orthogonal?

Environmental Resource Limitation

The perceptual vector of a single control unit projects onto a single dimension of environmental space, in which it defines the Controlled Environmental Variable of the control unit. The output projects onto another dimension of the environment--meaning that it affects aspects of the environement other than those of which the perceptual vector is composed. If the control system is efficient, its output vector correlates well with its perceptual vector, but nevertheless, the two vectors will almost certainly not be identical. Each individual control system therefore spans two dimensions of the environmental space.

The 2-D subspace of the environment spanned by the vectors of one control system will probably be nearly orthogonal to those spanned by another control system under two conditions: that the environment has enough dimensions (degrees of freedom) and that the two systems have reorganized together long enough to allow orthogonalization to happen.

In a mutual support domain, the individual control units are as orthogonal as are any other units. Participating in the same loop of mutual support does not mean that two control units are likely to have correlated vectors. If anything, the converse is true, since having correlated vectors would mean that the actions of one control unit would disturb the other's perceptual signal. So, if anything, the vectors of two units in a mutual support domain are more likely to be orthogonal than are those of two randomly chosen control units.

In a loop consisting of N units, the loop as a whole spans 2N dimensions of the environmental space in which perceptions and actions are made manifest. But one has to ask how many dimensions the environment has available. If there are L loops, is it reasonable to expect 2N*L dimensions to be available, so that all the N*L control units can avoid interfering with each other's attempts to control?

This is a question about resource limitation.

Resource Limitation and the growth of Societies

Control units in the same loop are highly unlikely to interfere with each other. But what happens if a control unit in one loop has its action vector correlated with the perceptual vector of a control unit in another loop? One or both of two things is likely to happen. Either reorganization will alter the vectors of one or more of the constituent control systems, or the deleterious effects will be dominated by shielding effects one loop provides to the other. Much as one individual control unit may shield another, so it is possible for one loop to shield another--though perhaps not very likely for any two arbitrary loops.

How can reorganization maintain orthogonality?

Remember that the control systems we are considering may all be in the same organic body, each in a different body, or they may be partitioned among a few distinct bodies. It is clearly more probable that a mutual support loop will evolve when the environmental relationships among the control units are stable, and that is most likely to occur when all the control units involved are in the same body. This provides the first possibility for mutual support domains to avoid interfering with each other--one body simply moves to a different part of the environment, physically.

Moving physically is neither necessary nor sufficient. Orthogonality means affecting different degrees of freedom in the environment, or in other words not influencing what the other is trying to influence. The problem arises when there are not enough degrees of freedom available to allow all the control systems to succeed at once. For example, both may need the same small quantity of available food, or to use the same telescope at a viewpoint. Then if one gets the food or the telescope, the other cannot. If there is plenty of food, or many telescopes, the environmental degrees of freedom are enough to allow the control unit vectors to be orthogonal. Otherwise there is a problem of resource limitation.

Resource limitation always means a lack of enough degrees of freedom for independent action by all the control systems under consideration.

Formation of Societies at many size scales

If the actions of the control units within one loop are not independent of the perceptions of the control units in another, at least one of the loops has constituents that influence the behaviour of the other. One can talk not of the control units interacting, but of the loops, as if each loop (support domain) were a unitary entity. The influence of one loop on another may be beneficial or detrimental, as it is when two elementary control units interact. But since the control exercised by an entire loop spans many dimensions, the influence of one loop on another can be simultaneously detrimental and beneficial.

Whether the influence of one loop on the control effectiveness of another is beneficial or otherwise, the mutuality structure within the influenced loop is liable to be altered. At one extreme, the loop itself may be destroyed, or, at the other, some pathways that have a common effect may change their emphasis.

Reorganization will occur if the influence of one loop on another impairs the ability of any constituent to control. The immediate result is likely to be reduced stability, but the end result will be enhanced stability, either by effective separation of the loops (orthogonalizing them), or by accommodating each to the other to form cooperative structures in the same way as control units may cooperate to form mutual support domains--and with enough interacting loops, the cooperative structures may deserve the name of "societies." In a society of loops, each has its own function, just as each elementary control unit has its own function in the operation of the loop. The entities in the societies have their own roles to play. As was pointed out earlier, in a well functioning society, those roles do not overlap--the individual control units in a loop control largely orthogonal perceptions, and happen to shield each other from external disturbances while doing so.

One can see this process continued recursively--and we do, in the form of cells, multicellular organisms. families and tribes, clubs, businees, unions, cultural and national groups...

Bottom Line

If the environment is sufficiently stable to allow the beneficial effects of side-effect shielding to continue, then:

Systems of large numbers of control units tend to self-organize into modular structures.

Although the structure may initially conflict or inadvertently disturb one another, "reorganization" brings their relationship into a configuration in which they largely support one anothe. These configurations are marginally stable. When confronted with novel influences such as the presence of a new module, they may be destroyed, change radically, or change only subtly.

Changes in one module may induce changes in its neighbours, creating the likelihood of "sandpile avalanches," in which the magnitude of change is totally unpredictable. But after a change, of whatever magnitude, eithe the systems will have been destroyed or a new organization will have been created, in which cooperation, not competition, is dominant.

Cooperation and conflict are inherent in Powers' insight that "All behaviour is the control of perception."

But in the end, cooperation will win over competition.