Quick Overview
 Control
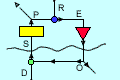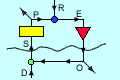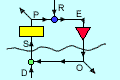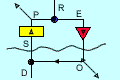
is taken to be the action of a "control unit". A Control unit takes inputs S
from its environment and provides output O that influences the environment so
as to affect the state of its inputs (among possibly many other aspects of the
environment). The inputs are also influenced by events in the environment of
which the control unit has no independent knowledge. These are known as "disturbances"
D. The inputs S are converted by a "Perceptual Input Function" into a scalar
perceptual signal P which may also serve as an input to other control units.
The control unit has a second input, a reference signal R, with which P is compared.
The difference between the values of P and R is known as the "error" E, which
provides input to an "Output Function" that delivers the output O. O influences
S through what is known as the "Environmental Feedback Path." If the influence
of O on S is such as to reduce the error E, the value of P tends to track the
changing values of the reference signal R. P is the "controlled perception"
of the control unit.
Control
is taken to be the action of a "control unit". A Control unit takes inputs S
from its environment and provides output O that influences the environment so
as to affect the state of its inputs (among possibly many other aspects of the
environment). The inputs are also influenced by events in the environment of
which the control unit has no independent knowledge. These are known as "disturbances"
D. The inputs S are converted by a "Perceptual Input Function" into a scalar
perceptual signal P which may also serve as an input to other control units.
The control unit has a second input, a reference signal R, with which P is compared.
The difference between the values of P and R is known as the "error" E, which
provides input to an "Output Function" that delivers the output O. O influences
S through what is known as the "Environmental Feedback Path." If the influence
of O on S is such as to reduce the error E, the value of P tends to track the
changing values of the reference signal R. P is the "controlled perception"
of the control unit.
If there are two control units controlling quite unrelated perceptions, there
is some chance that one of them might affect one of the environmental paths
of the other. Its side effects might act as a disturbance to the other, it might
be controlling something that is in the feedback path of the other, or it might
be controlling something in the path from the disturbance source to the other's
CEV. The chance of any of these happening may be very small for any specific
pair of control units, but the number of pairs goes up with the square of the
number of units, and so does the probability that there exists at least one
pair in which the actions of one unit affect the performance of the other.
With enough independent units, the probability approaches unity that there
exists at least one pair of units in which the actions of one unit helps the
other to control. We are interested only on those interactions in which one
unit acts to ease control by another, because reorganization will tend to eliminate
the other interactions insofar as the environment makes that possible.
Add a few more units, and the probability is high that there are many cross-influencing
pairs. This probability goes up fast since the number of available pairs increases
with the square of the number of units. And add yet a few more, and some of
the ones that ease the ability of others to control will become part of a chain.
A eases B and B eases C. With enough units, at least one such chain will form
a loop of mutual support. How many is "enough" depends on the probability that
any one will aid any other. Kauffman (At Home in The Universe, Oxford University Press, 1995) talks in terms of probabilities on the
order of 10^-6, to give you an idea.
I often use a somewhat strained example to illustrate a two-link loop. Imagine
a small ship in a choppy sea. The cook tries to deep fry a succession of batches
of food, but the motion of the boat means he can use only small quantities of
oil, to avoid splashing. The helmsman tries to keep a straight course, which
would help the cook if it could be done, but the waves make keeping straight
rather difficult.
Now the cook tosses his used oil overboard. That smooths the waves a bit, making
it easier for the helmsman to keep the boat on course. That makes it easier
for the cook to use more oil for the next batch of fry-up, which means more
oil to smooth the waves for the helmsman, and so forth. Neither knows anything
of the effect his actions have on the other, but so long as the cook keeps cooking
and the helmsman keeps steering, both have an easier job than if the other was
off-duty.
Such loops of mutual support must occur if there are sufficient numbers of
independent control units working in a constrained environment, no matter how
small the probability that the actions of one will help another to control.
In fact, Kauffman shows that in the generic case, there is a phase transition
at some number N, where below N the probability is near zero, and above N the
probability is near unity, with almost everything linked to everything else
directly or indirectly.
So far, the association of control units in a mutually supportive loop is purely
accidental. But think what happens if there is only one such loop and one of
the control units in it is removed. All of the control units in the loop then
find that their work is more difficult--not just the one immediately influenced
by the one that went missing. Less drastically, if one reorganized so as to
produce different side-effects, it would find that its own control became
more difficult (because it broke the loop), and would be likely to reorganize
back again (although the other loop members, finding their control diminished,
would also be reorganizing, until some new loop might form rather than the old
one re-forming).
Such loops must be self-stabilizing, in the same way that adding a second level
of control aids the work of the first-level controllers in a hierarchy. Subordinate
loops may, for example, exist to restore gaps in the loop. We begin to get into
social structures self-organized firstly by the purely random occurrence of
assistance loops, and secondarily by the process of reorganization.
Now consider loops built not with individual control units, but with hierarchic
organisms. A new-born organism is born into a "society". If the baby organism
acts in certain ways, the other members of the society act in ways that bring
the baby's perceptions near their reference levels. If the baby acts in other
ways, the other members of the society act so that at least some of the baby's
perceptions move away from their reference levels (if you want to call that
"coercion" it's fine by me; it's just what always happens in any environment,
whether that environment consist of other control systems or of inanimate objects).
The baby tends to reorganize so as to avoid the actions that spoil its ability
to control. Or to put it another way, it learns to be a "responsible" member
of the society. It has no "intrinsic variable" need for socialization, but if
it does socialize properly as expected for its age, it gets its perceptions
better under control than if it doesn't. It helps others, and they help it.
It learns the language and the culture into which it is born, as if there were
some innate drive for it to do so, though there need be none.
(Parenthetically, one may argue that helping one another without expectation
of a direct quid pro quo is the mature expression of this. It results in the
same kind of mutual support loops that benefit everyone as those I discussed
a couple of paragraphs ago. That's why I consider Jesus as one of the great
economists of history, when he said "Cast your bread upon the waters, and it
will return to you many times over." Or something like that. It's the antithesis
of the economic theories that blight our current global economy by starving
the poor, since they are based on getting the most you can and giving the least).

 Control
is taken to be the action of a "control unit". A Control unit takes inputs S
from its environment and provides output O that influences the environment so
as to affect the state of its inputs (among possibly many other aspects of the
environment). The inputs are also influenced by events in the environment of
which the control unit has no independent knowledge. These are known as "disturbances"
D. The inputs S are converted by a "Perceptual Input Function" into a scalar
perceptual signal P which may also serve as an input to other control units.
The control unit has a second input, a reference signal R, with which P is compared.
The difference between the values of P and R is known as the "error" E, which
provides input to an "Output Function" that delivers the output O. O influences
S through what is known as the "Environmental Feedback Path." If the influence
of O on S is such as to reduce the error E, the value of P tends to track the
changing values of the reference signal R. P is the "controlled perception"
of the control unit.
Control
is taken to be the action of a "control unit". A Control unit takes inputs S
from its environment and provides output O that influences the environment so
as to affect the state of its inputs (among possibly many other aspects of the
environment). The inputs are also influenced by events in the environment of
which the control unit has no independent knowledge. These are known as "disturbances"
D. The inputs S are converted by a "Perceptual Input Function" into a scalar
perceptual signal P which may also serve as an input to other control units.
The control unit has a second input, a reference signal R, with which P is compared.
The difference between the values of P and R is known as the "error" E, which
provides input to an "Output Function" that delivers the output O. O influences
S through what is known as the "Environmental Feedback Path." If the influence
of O on S is such as to reduce the error E, the value of P tends to track the
changing values of the reference signal R. P is the "controlled perception"
of the control unit.