This note is based on a posting I made to CSGnet March 3, 1998
The recent reincarnation of the discussion on the relation between the disturbance signal and the perceptual signal has made possible an interesting analysis. We can compute, at least for the simplest control loop with a perfect integrator output function, the maximum possible correlation between the two signals, as a function of the degree of control. If my analysis is correct, this maximum is 1/CR, where CR is the control ratio--the signal in the absence of control to its amplitude when control is in operation. The correlation would be lower, if there is noise in the system.
I'll make a large caveat here. To me, this analysis seems too simple, and I'd be grateful if anyone can find an error that increases the maximum correlation possible between p and d in this idealized maximally simple control loop, or show by simulation that the actual correlation is higher than the analysis shows. I submit the analysis because I can't by myself, see anything wrong with it, other than approximations that work in the direction of increasing the maximum.
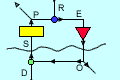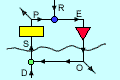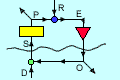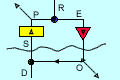
We start with the classic diagram
of a control system:
And we will make the usual assumptions that are made when using the expression "p = o + d". That is to say, all the functions in the loop except the output function are unit transforms.
Since it is short, I will repeat the standard loop derivation, working backwards around the loop from the perceptual signal (in this case equal to s, the sensory signal):
p = o + d = Ge + d = G(r-p) + d = Gr - Gp + d (where G represents the output function)
which yields d = p + Gp - Gr.
That's starting point 1.
In the equation, d = p + Gp - Gr, all the "variables" are actually Laplace transforms, which can be treated as if they were algebraic variables if the system is linear (an integrator is a linear system). A Laplace transform is a way of describing a time function, to put it crudely. The output function, G, is a pure integrator in the example I analyze below.
Starting point 2:
If the output function is a pure integrator, all frequency components are phase-shifted by 90 degrees, which reduces the correlation to zero. The Fourier transform of the signal consists of a set of components of the form ancos(nt+ø), for which the integral is ansin(nt+ø). Each component is therefore uncorrelated with its integral, and by the construction of the Fourier transform, is also uncorrelated with any of the components at other frequencies. Hence the overall correlation is zero.
For now, I'll consider only the case with a perfect integrator output function, but the argument works (giving a different final result) with any function. One just has to know the correlation between the function's input and output. For G a pure integrator,x the input and output are uncorrelated. For other functions, the correlation is likely to depend on the frequency spectrum of the input of the function.
Firstly, note that symbols like "p" and "d" represent waveforms extended over a long (notionally infinite) time. I use the same symbol also to represent the Laplace transform of the signal. When the signals are treated as vectors and we talk of correlation, the time variation (the waveform) is what you should think of. In developing the equations (e.g. "d = p + Gp - Gr") the Laplace transforms are used. The two are essentially interchangeable in the current context, which is why I haven't worried about my inability to use the conventional script font for the transform.
If G = 0 (no output from the control unit, and hence no control), p = d. Clearly then the correlation between p and d is 1.0.
To start the next phase of the derivation, consider the case of r = 0 forever. In this case, Gr (the integral of r) is also zero forever, and d = p + Gp -Gr reduces to
d = p + Gp,
which
is a vector addition, as shown in the diagram. Using
the assertion that a variable is uncorrelated with its integral, the variable
"d" is composed of two orthogonal components, p and Gp (remember, "G" is the
output function, which is assumed to be a perfect integrator).
The squares of the lengths of the vectors represents the mean-square amplitude variation in the signal values. When you think of the variations on this diagram that occur as the output gain changes, or as the reference signal is allowed to vary, remember that it is the "d" vector that stays constant, while the others may change their magnitude and direction--not the other way around.
The correlation between any two vectors is the cosine of the angle between them. That is why Gp and p are drawn at right angles. Their correlation is zero. If Gp is large compared to p, d has a correlation of nearly 1.0 with Gp and nearly zero with p. Since we are dealing only with the case in which the reference signal is fixed at zero, the output signal is Ge, which is -Gp. So the disturbance signal is correlated almost -1.0 with the output signal--as we know to be the case for good control.
The control ratio (CR) is the ratio between the fluctuations that would occur in p in the absence of control and the fluctuations in p when the perception is controlled. In other words, CR = d/p when the transform between s and p is the unit transform. The cosine of an angle in a right-angled triangle is the length of the opposite side over the hypotenuse. That is to say Corr(d:p) = p/d. From this, the correlation between d and p is 1/CR.
Why did I say this was a maximum correlation rather than the precise correlation? In part this is because there is always noise, but more because of the role of the reference signal. Above, we considered the case of r permanently zero. Now we let r vary, independently of d, of course.
The control system is linear. What this means is that the superposition theorem holds--the contributions of different components can be added in the time domain, in the frequency domain, and in the Laplace domain. In particular, the relation d = p + Gp can be used as a starting point, onto which can be added any effects due to the variation of r. Most importantly, p and Gp will change when r varies. Gp (the integral of p in the simple system we are analyzing) can, because of superposition, be divided into two parts, which I will label G_d.p and G_r.p. G_d.p is just what we had before, when r was fixed permanently at zero. G_r.p is the variation in Gp that is extra, due to the variation in r.
Now we can look at the full expressions that was shown above:
d = p + Gp - Gr
and rewrite it
d = p + G_d.p + (G_r.p - Gr)
The first part of this is exactly what we had before, when r was permanently fixed at zero. The part in brackets is the contribution of variation in r. What does the part in brackets contribute to the correlation between d and p? Since the reference signal varies independently of the variation in the disturbance signal, and any contribution of (G_r.p - Gr) is due to the reference signal, that contribution is orthogonal to d (and to G_d.p). It cannot increase the correlation between d and p, except by accident over the (very) short term. Furthermore, the better the control, the more nearly does p match r, and therefore the more nearly does G_r.p match Gr. The two tend to cancel one another, so if they have an effect, it tends to become small when control is good.
What this means is that even when the reference signal is allowed to vary freely, the maximum correlation that should be observed between the perceptual signal and the disturbance signal is 1/CR.
The above applies mathematically only to a control system that is linear, has no loop transport delay, has a perfect integrator as its output/feedback function, and has no other time-binding functions in the loop (i.e. all the other functions are simple summations or multiplications by constant factors). Most control systems are not like that. What then?
Some cases can be examined heuristically. For example, if the output function G is a leaky integrator rather than a perfect integrator, the angle between p and Gp depends on the frequency spectrum of p. If low frequencies dominate, then Gp correlates well with p, but if high frequencies dominate, G acts like a good integrator. So the correlation between d and p can be greater than 1/CR if the output function is a leaky integrator.
If there is some loop transport delay, it has to be incorporated into the initial expression for d. It could all be included in the output function, G. With loop delay, the correlation between the input to G and its output will vary between positive and negative correlation as a function of the frequency of p. This will show up in a correlation between Gp and p that varies with the spectrum of p. In the diagram, Gp would lean left and right as the frequency of d varies. If the magnitude of G is large enough, this can lead at some frequencies to p being larger than d. In such a case there is no control, and the cosine takes on an imaginary (or at least complex) value. The loop is oscillating, not controlling.
Other cases can be examined similarly, provided the system is composed of linear components that allow the use of Laplace transforms. And for some non-linear systems one can make reasonable heuristic approximations by appealing to small-amplitude linearity.